수학으로 배우는 파동의 법칙 - 정리

[1] 큰 목소리 – 파동이 높다. – 진폭이 크다.

작은 목소리 – 파동이 낮다. – 진폭이 작다.

높은 목소리 – 파동의 폭이 좁다 – 진동수(주파수;Hz)가 높다 – 짧은 주기(T)

낮은 목소리 – 파동의 폭이 넓다 – 진동수(주파수)가 낮다 – 긴 주기

[2] 사람의 듣는 주파수 20Hz~20000Hz 정도까지 들린다? (50p)

[3] 기본주파수 – 각각의 진동수를 갖는 파동의 합쳐졌을 때, 그 안에 포함된 가장 커다란 파동의 주파수

A(2Hz), B(4Hz), C(6Hz), D(8Hz) => 2Hz가 기본주파수가 된다.

[4] 이론상 2n개의 좌표를 알면 n개의 진동을 수할 수 있다. – 178p

[5] 어떠한 파동을 나눌때 그 구간이 달라지면,(ABCABC 이런 파동일때 ABC를 한구간으로 보느냐, BCA를 하구간으로 보느냐) 푸리에 계수값이 변한다.( 179p)

$\begin{align*} d_n=\sqrt{a_n^2+b_n^2} \end{align*}$

그러나 위 처럼 구한 벡터의 크기(진폭)은 거의 맞아 떨어지게 된다.

(5) 푸리에 계수

$\begin{align*} a_0&=\frac{1}{T}\int_{0}^{T}f(t)dt \\ a_n&=\frac{2}{T}\int_{0}^{T}f(t)\cos(nwt)dt \\ b_n&=\frac{2}{T}\int_{0}^{T}f(t)\sin(nwt)dt \end{align*}$

[6] 인간의 인지는 로그 함수와 같다.
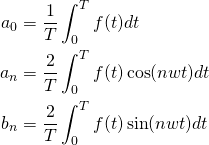
110Hz의 한옥타브 높은 주파수는 220Hz, 그 다음 한 옥타프 높은 주파수는 440Hz

[7] 큰 목소리와 작은 목소리의 경우 각 formant의 절대값은 달라지나 비율은 유지된다.

[8] 오일러 공식(이해가 어려운 파트)

(1) $\begin{equation*} C(x) &= \cos(x) + i\cdot\sin(x) \end{equation*}$

(2) $\begin{equation*} f(x) &= e^{ix} \end{equation*}$

(3) $\begin{equation*} f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + \cdots \end{equation*}$

(4) $\begin{equation*} f(x) = \sum\limits_{n=0}^\infty \frac{1}{n!}f^{(n)}(0)x^n \end{equation*}$

(5) $\begin{align*} e^{ix} &= \cos(x) + i\cdot\sin(x) \\ e^{-ix} &= \cos(x) - i\cdot\sin(x) \end{align*}$

(1): 가우스 평면(복소수 좌표)에서 원을 그리는 함수
(2): 4차 미분시 원래의 $f(x) = e^{ix}$ 가 되는 함수
(3)의 공식을 미분을 이용하여 계수를 구하여 풀어내면 (3)의 식이 되는데, 이것을 매클로린 전개공식 이라고 한다.
(1)와 (2)의 식을 매클로린 전개하면 같은 값(계수)이 나온다.
(5)가 오일러의 공식이다.

그러나 사실 이러한 공식을 알 필요는 없을 듯 하나, 직접 푸리에 계수를 전개할 필요는 없으니
다만 FFT 함수를 이해하는데 도움이 되려나.

[9] 비주기 파동의 분석

$\begin{equation*} \Delta f = \frac{1}{T} \end{equation*}$

기본 주파수 f 는 주기(T)에 반비례 한다.
이 때, 비주기 파동의 경우 주기가 무한히 길어지는 것이기 때문에

$\begin{equation*} \Delta f = \frac{1}{\infty} \end{equation*}$

즉, 한 주기를 돌 때 무한한 시간이 걸린다면, 그 주파수는 0에 가까워 지는 것이다.
기본 주파수에 0에 가까워 진다면, spectrogram에서 각 주파수(기본 주파수의 n배가 되는 주파수들)의 간격이 점점 가까워져서 전체적인 윤곽을 보는 양상이 될 것이다.
책의 페이지 498~511까지는 이 비주기 파동의 분석을 위해 오일러 공식을 이용해서 풀어나가는데, 이해하기 쉽지 않다.
결론의 512페이지에 있는데,

즉, 비주기 파동을 분석하기 위해서는 ‘관찰시간’이라는 개념을 사용한다. 짧은 시간 ( $\Delta t$ )의 관찰을 통해 전체적인 주파수의 특징을 이해하는 방식이다. 이 경우 재미있는 특징이 관찰되는데, ( $\Delta t$ )가 커질 수록 ( $\Delta f$ ) 가 작아지게 된다.

책에서 예를 든 공식은 $f(t) = 1$ 이라는 함수(즉 어느 시간에도 주파수가 1), $G(f)$ (푸리에 변환된 함수;이 때에 f(0)(기본주파수)만 값이 있는 직선 함수가 나온다). 이를 푸리에 변환시키면 이상적으로는 직선이 나와야 하나, 일종의 파동 그래프 처럼 나온다. f(0)에 $\Delta f$ 가 존재하게 되는데, 이 것이 ‘불확정성’이라고 이야기 하게 된다.
즉 ( $\Delta t$ )가 커질 수록 ( $\Delta f$ )는 작아지고, 그 반대가 성립하는 양자역학의 범위까지 넘어가게 된다.

[10] FFT
Nyquist-Shannon sampling theorem 이랑 같은 것인지는 모르겠지만, 어찌되었든, 어떠한 주파수까지(예:0~4000Hz)까지 분석하고 싶으 파형이 있다면, 그 파형(아날로그)의 점들(디지털값)이 그의 2배인 8000개가 필요하다.
보통 음성분석에서는 20-40 msec을 한 프레임으로 잡는 듯 한데(왜인지는 여전히 검색중) 40msec으로 한다면 320개의 점이 필요하다는 이야기이다.

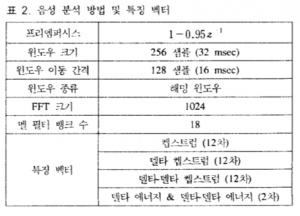
어떤 논문에서 따온 표이다. 보면 32msec동안 256샘플을 썼다는 이야기는, 1초로 보면 8000개의 포인트 즉 4000Hz까지 분석하겠다는 이야기가 된다.

40msec으로 돌아가서, 이 경우 320개의 점이 찍혀있고, 이 시간동안 160개의 진동하는 주파수들을 분석한다면,
사람이 실제로 그 그래프를 직접 적분한다면 320×160=51200의 곱셉이 필요하게 된다.(고한다;;)
그러나 실제 계산에서 보면 $e^{ix} &= \cos(x) + i\cdot\sin(x)$ 함수는 회전함수이기 때문에 이 오일러 공식으로 나온 푸리에 계수 구하는 공식은 그 계수값이 공통되어 곱셈횟수를 획기적으로 줄일 수 있게 된다. 세부내용은 생략해도 될 것 같다.

그래서 음성 분석시 4000Hz라 한 frame(40mesc)에 320개의 점이라고 할 때, 실제로는 512나 1024 ( $2^n$ )개의 숫자로 FFT를 돌리는 것이 더 빠르다고 한다.

수학으로 배우는 파동의 법칙 – 정리

Like this:

J Seok

Leave a Reply Cancel reply

[LaTex] 수직 그래프(x=n)

[LaTex] Arc