음성 음향 분석론 – 정리

책: 음성 음향 분석론, 제2판, 박학사

[1] 분석 목적으로 이용되는 최소 시간 분해대는 약 10ms, 자음의 개방(release)와 관련된 순간음 파열(transient burst)와 같은 중요한 음성결과에 대한 가장 짧은 구간이다.(pat, cat, tat 등의 첫 음들)
음성 신호의 대부분은 10kHz의 범주에 분포하며 60dB 정도의 dynamic range, 10ms나 혹은 그 이하의 중요한 변화를 담고 있다.(16p)

[2] 비음은 모음처럼 전형적으로 음원 에너지로서 유성성(vocing)을 지닌다. 차이가 있다면 음원 에너지가 구강 및 비강 양쪽에서 결정된다.(20p)

[3] 음원 여과기 이론
: 방사된 음성의 음성 압력 스펙트럼, s 를 frequency(f)로 이해할 수도 있다.
: 후두 음원 스펙트럼 – 후두 음원은 기본 주파수()의 배음(harmonic components)로 구성되는데, 에너지 감소 비율은 한 옥타브당 12dB (주파수가 2배가 되면 12dB이 감소), 사람에 따라 다르다.
: 성도 전이 함수 – 포만트로 이루어진 그래프 (LPC 그래프로 생각하면 될 듯하다)
: 방사 특징(radiation characteristics) – 음성이 대기로 방출될 떄 일어나는 여과 효과로, 고주파 통과기와 유사하여 옥타브당 6dB 정도로 주파수가 증가한다. 후두 음원 스펙트럼의 옥타브당 -12dB과 방사특징의 +6dB는 함께 계산되어야 한다. (25-28p)

[4] : 혀 높이(tongue height)로 역으로 바뀜(고모음 /i/,/u/ – 저주파수, 저모음 /a/,/æ/ – 고주파수)
: 전방, 후방 – (후설모음 /u/,/a/ – 저주파수, 전설모음 /i/,/æ/ – 고주파수) (31p)

[5] 입술을 모으는 행위 – 성도의 길이가 길어짐 – 주파수는 낮아짐, 영어에서 전설모음은 원순모음이 아니다. 전체적인 주파수를 낮추는 경향이 발생함(32p)

[6] Formant : 극점(pole) – 에너지의 강화
Antiformant : 영점(zero) – 에너지의 손실 (48p)
(두 쌍의 용어를 책에서 사용한 이유는 formant, antiformant가 성도에 사용되는 용어-즉 모음-라면 자음 분석에 사용되는 비슷한 개념을 표현하고 자 사용했다. 그러나 자음 분석은 조금 이해하기 어려운듯 하다)

[7] Wavelet 변형(59p)
https://www.youtube.com/watch?v=QX1-xGVFqmw&t=196s
책만 보면 이해가 잘 안가지만, 동영상을 보고 나니 약간 이해가 되는 부분이 있다. 즉 웨이브렛은 확대하거나 축소할 수 있는 조그만 파형이다. 복잡한 음향이 다양한, 그리고 확대와 축소가 가능한 웨이브렛으로 분석될 수 있다는 것이다.
(책의 3장에 있다고 하니 더 봐야겠다)

[8] 음성 신호의 처리에서 기본적으로, 여과(filtering), 표본추출(sampling), 양자화(quantization)을 거친다.

[9]  74p, Nyquist’s sampling Theorem에 따르면, 우리가 분석할 주파수의 2배의 표준 추출률(smapling rate)가 필요하다는 것이다. 이야기인 즉슨,

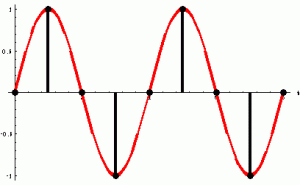
출처:http://microscopy.berkeley.edu/courses/dib/sections/02Images/sampling.html

상단에서 볼 수 있듯이 우리가 분석할 그래프의 최대점과 최소점을 알아야 하나의 그래프가 그려지게 된다.

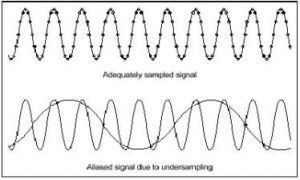
만약 그렇지 못할 경우, 아래그림에서 보면 밑에 그림과 같은 현상이 발생하게 된다. 표현하자면, 실제의 고주파수가 저주파수로 인식되어버리는 현상(aliasing)이 나타나게 되며, 아래 스펙트럼 분석 표를 보면 sampling rate 가 분석 주파수를 100으로 잡았을 때 그의 절반인 50Hz보다 큰 주파수에 대해 발생하는 alise들을 표시하였다.

 

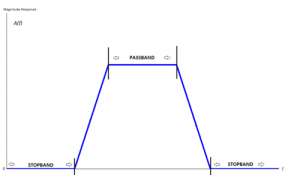
Filtering에서 pass band는 우리가 분석하고 싶은 주파수를 포함해야 하고, 이것이 바로 stop band로 낮아지지 않고, Guard band라는 공간이 발생한다.

(출처: 위키피디아)

이것으로 부터 Sampling rate에 대한 이야기가 시작되는데,

http://www.alanjshan.com/sampling-01/ 의 설명을 참고해서 이해하면 다음과 같다. 일반적인 음반에서 Sampling rate가 44.1kHz가 되는 이유를 이렇게 설명할 수 있을 것이다. 20kHz 까지의 음악 주파수를 담기위해 40kHz까지 pass band를 만들어야되는데, 이에 대한 guard band로 인해 44.1kHz의 sampling rate가 나오는 것이다.

아무튼 결론적으로, 다음과 같은 순서로 sampling을 진행한ㄷ.

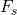1. 을 설정
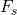2. 이상의 에너지를 여과(filter; low pass filter라고 한다)
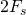3. 비율로 신호를 표본화한다.

[10] 88p. 파형 절단에 대해 – 어떠한 절단도 공동 조음(coarticulation) 때분에 자연스럽지 못하다. 어떤 모음에서 자음을 분리해도, 모음은 그 자음의 전이 부분을 포함하거나 최소한의 조음 위치가 포함됨. 파형이 크게 양(+), 음(-)인 곳에서 절단은 돌발소음(popping sound;음향전이)를 만들어낸다. 전문적인 절단 연구자는 영점선상(zero line), 동일 진폭의 양측 끝에서 결합한다.

[11] 98p. Frame은 보통 20~30ms(두개 혹은 세개의 성문주기를 포함)한다. 프레인 구간(interval)은 연속된 프레임의 중복되는 정도, interval이 너무 작으면(중복이 크면) 불필요한 입력이 일어나고, 너무 크면(중복이 너무 작으면) 급격한 변화를 놓칠 수 있다.

[12] 107p. 다양한 값을 구하는 방식에 대한 서술이다. Spectrograph, Cepstral analysis, Autocorrelation, etc. 등.

[13] 이후 책의 4장, 5장은 모음, 이중모음, 자음 등의 각론, 6장은 여성, 어린이의 음성 분석과 관련된 내용을 담고 있다. 정리하게에 조금 복잡하고 방대한 내용들로 일단 여기서 멈춘다.(2017.7.25)