푸리에 해석 – 기초 공부

• 참고서적 : 만화로 함께 배우는 푸리에 해석, 성인당

<기초지식 1>

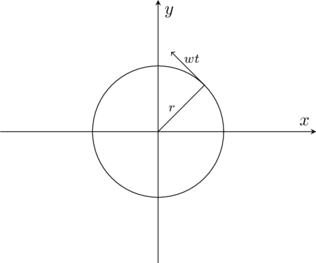
진동을 원으로 표현하면, 위의 그림과 같이 나타낼 수 있다. 위의 , 를 따로 나타내보면

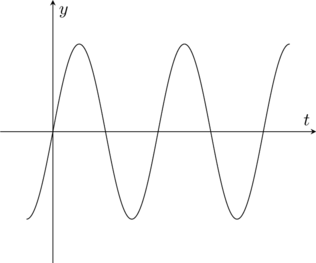
와 의 관계는 위의 그림처럼 나타낼 수 있고, 와 의 관계는 아래와 같다.

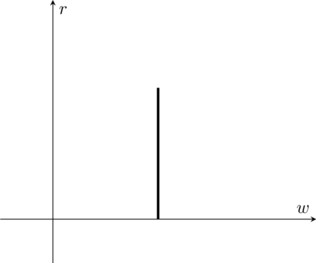
<기초지식 2>

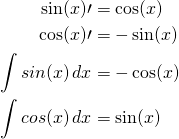
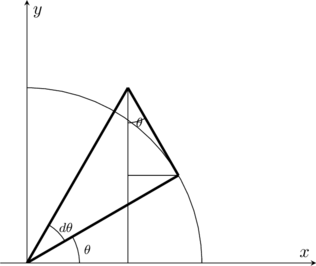
삼각함수의 미분은 를 과장하여 확대했을때 그려지는 삼각형을 이용해서 구하면 된다. 반지름 1의 원을 기준으로 하면,  인데, 를 각으로 갖는 작은 삼각형의 빗변이 인 것은 반지름의 1인 삼각형에서 라디안 값을 갖는 원호(arc)의 길이는 똑같은 이기 때문이다.

물론 이 그림에서 원호가 아닌 삼각형으로 나타낸 것은 미분 유도를 위해 를 과장해서 표현했기 때문이다. ( 는 사실 접선의 기울기! = 각속도())

요런 함수들을 알면 좋다.

<기초지식3>

직교 상태라는 것은 벡터에서 내적이 0이라는 것으로, 두 벡터의 사이각이 이라는 이야기다. 직교 상태의 벡터의 내적은 항상 0인데, 즉 직교 상태의 함수의 곱의 정적분도 항상 0이 된다.
이 부분에서 정적분을 이야기 할 때에 그 범위는 0에서 까지를 이야기 하게 되는데, 그 이유는
에서 n이 무엇이든지 간에 기준 주기를 의 주기로 의식하게 되어 0에서 를 단순 대입하는 것이 가능하다.

일 때, 는 와 항상 직교한다.
일 때, 는 와 항상 직교한다.
(증명은 생략, 삼각함수의 곱의 적분 공식 이용)
또한 의 정적분도 항상 0이 된다.

<기초 지식4>

위 함수에서 는 진폭, 는 주기를 나타낸다.

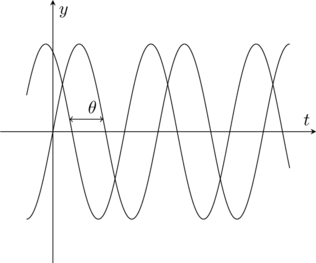
를 위상이라고 하는데 위 그래프의 경우 라고 나타낼 수 있지만, 푸리에 해석을 위해서는 로 구한다. 두 함수는 위에 서술한 바와 같이 직교하는 함수이기 때문에 다른 방식으로는 나타낼 수 없는데, 그 이유는 를 만족하는 값은 존재하지 않기 때문이다.

정리하자면 공식을 통해 변수 를 바꿈으로써, 주기는 변동하지 않으면서 진폭과 위상을 바꿀 수 있다.

진폭의 경우 벡터의 크기를 이용하는 방식으로,

다음과 같이 구할 수 있다.